Un pendule inversé sur chariot (régulation LQR)
Inverted pendulum on a cart – LQR controller
Cet article donne tous les détails techniques dont vous rêviez au sujet de ce pendule :
Fabrication / composants
Mécanique
Entrainement du chariot : moteur Pololu à CC avec réducteur 9.7:1 et encodeur rotatif 48 CPR intégré. Cet encodeur permet de connaitre précisément son angle de rotation.
Mesure de l’angle de la barre : encodeur rotatif incrémental photoélectrique 600P (E38S6G5-600B-G24N) de 2400 impulsions / tour. La barre est fixée directement sur cet encodeur.
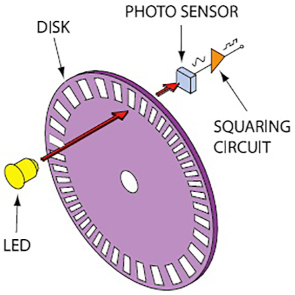
Un encodeur rotatif ?
Il permet de mesurer un angle de rotation. Dans mon cas, il est photoélectrique : cf. schéma ci-contre.
Pour connaitre le sens de rotation, il y a en fait 2 rangées de fentes, décalées. L’une produit un signal carré sur la sortie A de l’encodeur, l’autre sur la sortie B, déphasés.
Pour le reste, je vous laisse regarder les photos et la vidéo.
Les pièces blanches sont imprimées sur une Imprimante 3D Elegoo Neptune 4 Plus.
Electronique
Un dessin (détaillé) vaut mieux…
Cliquez sur l’image pour agrandir
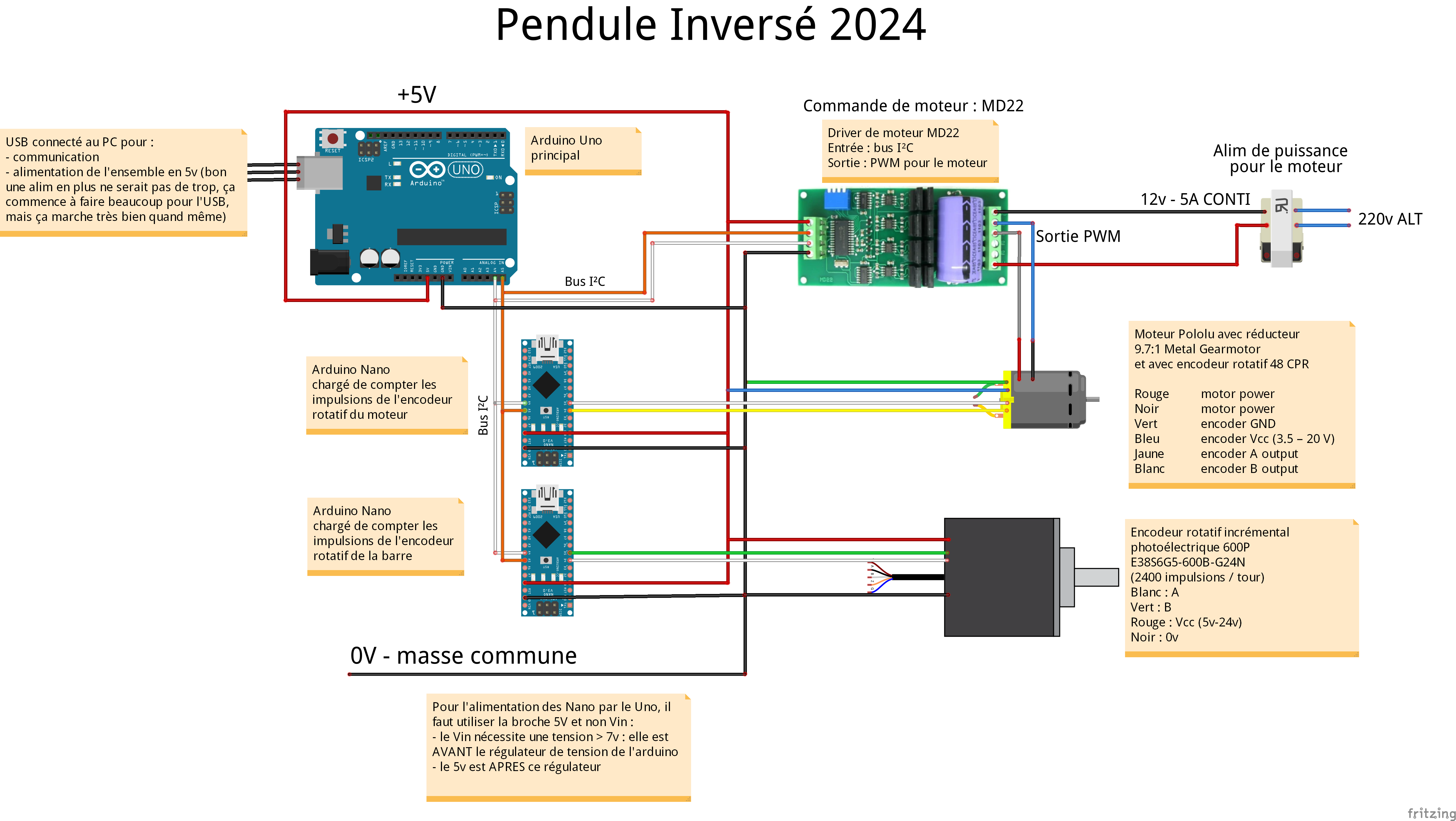
L’arduino Uno principal :
- récupère la position angulaire de la barre verticale en interrogeant l’arduino Nano dédié à cette tâche, via le bus I²C
- récupère la position angulaire du moteur en interrogeant l’arduino Nano dédié à cette tâche, via le bus I²C
- effectue les calculs de régulation à partir de ces données
- envoie la commande au moteur en passant par le driver MD22, via le bus I²C
- communique avec le PC via le port COM
- et tout cela… en boucle
Cet ensemble relativement simple fonctionne parfaitement !
Encodeurs rotatifs
Les 2 encodeurs rotatifs nécessitent une réactivité parfaite du circuit qui détecte les créneaux (impulsions A et B) qu’il produit. Un créneau loupé, et tout devient faux. Ce n’est pas très grave pour l’encodeur du chariot, mais beaucoup plus pour l’encodeur de la barre.
J’avais dans un premier temps tout connecté à un unique Arduino. Celui-ci devait donc gérer les 2 encodeurs, ainsi que les calculs d’asservissement. Cela ne fonctionnait pas, je perdais des impulsions.
J’ai donc fait le choix (peut-être un peu luxueux) de déléguer le comptage à 2 autres Arduino (nano) : un pour chaque encodeur. Ceux-ci communiquent alors leurs mesures à l’Arduino principal par un bus I²C.
Moteur
Le moteur est commandé par un « driver » MD22, très pratique : via le bus I²C on envoie :
- l’identifiant du moteur que l’on souhaite commander (1 ou 2. Car ce driver permet de commander 2 moteurs)
- la « puissance » et direction souhaitée : une valeur comprise entre -128 et +127
Le MD22 « convertit » cette information en un signal de puissance PWM envoyé au moteur.
Programmation : concepts généraux
Pour ce genre de projet, une IHM me parait indispensable. Elle permet de :
– modifier les paramètres (coefficients) du programme
– avoir une vue sur son exécution (mesures diverses…)
Je souhaitais malgré tout construire un système autonome (=qui fonctionne sans PC)
J’ai effectué le choix suivant :
- la régulation est effectuée par un Arduino Uno (langage C)
- cet Arduino Uno communique avec un PC par le port USB (qui devient un port série). Sur ce PC un programme écrit en C# présente une IHM permettant de :
- d’afficher les mesures de l’arduino (angle…) et d’autres informations
- modifier les paramètres pour ajuster les valeurs qui ont été calculées
- cet Arduino Uno communique avec 2 Arduino Nano chargés de compter (via un bus I²C)
Régulation
C’est ce qui m’a donné le plus de fil à retordre…
Les méthodes de régulation les plus courantes pour ce type de machine sont le PID et le LQR.
Régulateur « PID » (abandonné)
Le PID est le plus simple à mettre en œuvre. Il ne demande pas de calcul, et son réglage se fait manuellement, par essais / erreurs, en recherchant 3 coefficients : Kp, Ki, Kd. Son principe est assez simple à comprendre.
Je ne vais pas le détailler ici car… d’une part on trouve beaucoup d’explication sur internet, et d’autre part car je n’ai pas réussi à obtenir un résultat correct avec ce type de régulation. Pourtant j’y ai passé du temps… Mais c’est sûrement possible, car j’ai vu beaucoup de projets similaires sur internet, qui fonctionne avec un PID.
Régulateur « LQR »
Après des semaines d’échec avec le PID, je me suis tourné vers le LQR.
Bon alors au début, quand on commence à se documenter sur le LQR, franchement… on ne comprend rien (enfin pour ma part). J’ai trouvé des dizaines de thèses, mais je n’arrivais pas à comprendre le concept, et comment concrétiser le résultat sous forme de code. C’est finalement… ChatGPT qui m’a fourni les explications les plus claires (même si les calculs présentaient des erreurs)
Et au final, nous allons voir que le code est… très proche de celui du PID !
Mettre en œuvre un asservissement LQR (Linear Quadratic Regulator) s’effectue en plusieurs étapes, détaillées ci-dessous.
1 – Modélisation du système
Pour commencer, il faut parvenir à représenter le système dynamique sous la forme suivante :
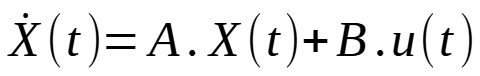
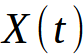 est le vecteur d’état (positions, vitesses… voir plus bas)
est le vecteur d’état (positions, vitesses… voir plus bas)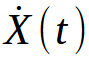 est la dérivée de X par rapport à t (donc la dérivée des composants du vecteur)
est la dérivée de X par rapport à t (donc la dérivée des composants du vecteur)- u(t) est le vecteur des entrées de commande : dans notre cas la force exercée sur le chariot par le moteur
- A est la matrice de dynamique du système
- B est la matrice de contrôle
Pas de panique, je vais tenter d’expliquer un peu tout ça.
Déjà, un petit schéma :
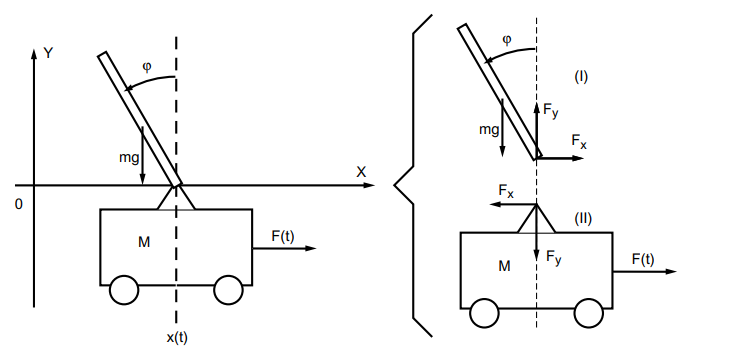
L’état de notre système est défini par les variables x et 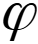 (lettre grecque « phi »)
(lettre grecque « phi »)
Dans notre cas pour décrire l’état de notre système, on choisit le vecteur X(t) suivant :
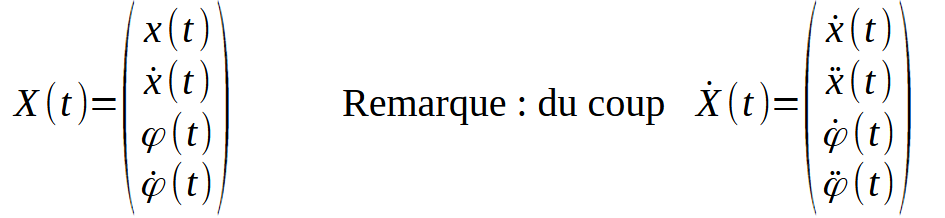
Cela est suffisant pour décrire la dynamique du système. Les accélérations peuvent être déterminées par les équations de la dynamique, il n’est donc pas utile de les inclure dans ce vecteur (sinon cela introduirait une redondance)
De plus, pour simplifier les calculs, il est nécessaire de choisir x=0 et 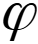 =0 comme valeur cible : le but de l’asservissement sera toujours de ramener x à 0 et
=0 comme valeur cible : le but de l’asservissement sera toujours de ramener x à 0 et 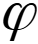 à 0.
à 0.
x=0 correspondra donc au milieu du rail du chariot, et 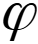 =0 à la position verticale de la barre.
=0 à la position verticale de la barre.
– u(t) est la force exercée sur le chariot par le moteur pour maintenir la barre verticale. J’ai considéré que la commande à envoyer au moteur (=la puissance) était proportionnelle à cette force. C’est un vecteur à une seule composante dans notre cas : notre système n’a qu’une seule entrée : la force exercée sur le chariot (par le moteur)
– A est une matrice 4 x 4 (car le vecteur d’état a 4 composantes) que nous allons déterminer ensuite, et qui dépend des paramètres du système : dimensions, masses…
– B est une matrice 1 x 4 qui dépend aussi des paramètres du système.
Pour parvenir à représenter le système sous la forme
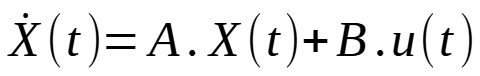
nous allons partir des équations dynamique du système.
Principe fondamental de la dynamique
Pour rappel :


Appliqué au balancier
Ce principe fondamental permet de calculer les accélérations.
Le détail des calculs (ainsi que le schéma ci-dessus) proviennent de cette thèse :
https://freddy.mudry.org/public/NotesApplications/na_pendinvc.pdf
Résultat trouvé dans cette thèse :
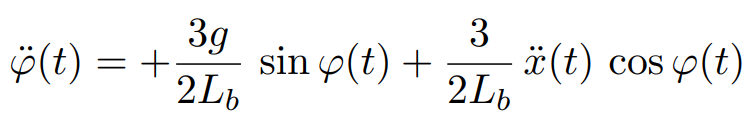
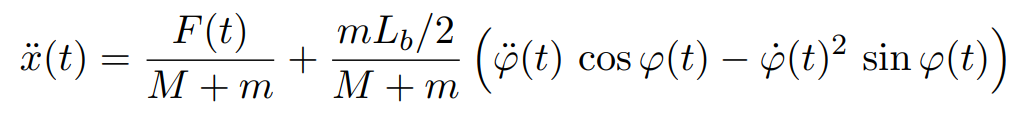
en négligeant les frottements.
Je ne détaille pas ces calculs, je suppose que vous connaissez ce principe fondamental de la dynamique (désolé, je ne peux pas tout détailler non plus…)
Les calculs ne sont pas trop compliqués. Et on peut comprendre la forme du résultat :
– ![]() : terme avec le sin() : la barre subit une accélération angulaire liée à son poids (g se trouve dans le terme). Et cette accélération est d’autant plus grande que l’angle est grand : si l’angle augmente, son sinus augmente.
: terme avec le sin() : la barre subit une accélération angulaire liée à son poids (g se trouve dans le terme). Et cette accélération est d’autant plus grande que l’angle est grand : si l’angle augmente, son sinus augmente.
– ![]() : terme avec le cos(), faisant intervenir
: terme avec le cos(), faisant intervenir ![]() : si
: si ![]() est grand c’est que le chariot accélère, ce qui induit aussi une accélération de l’angle jusqu’à ce qu’il atteigne 90°. Le cosinus intervient donc : cos(90°)=0 donc arrivé à 90°,
est grand c’est que le chariot accélère, ce qui induit aussi une accélération de l’angle jusqu’à ce qu’il atteigne 90°. Le cosinus intervient donc : cos(90°)=0 donc arrivé à 90°, ![]() n’influence plus
n’influence plus ![]()
– ![]() : terme avec F(t) : c’est logique, l’accélération du chariot est directement liée à F (principe fondamental…)
: terme avec F(t) : c’est logique, l’accélération du chariot est directement liée à F (principe fondamental…)
– ![]() : terme avec le cos(): si
: terme avec le cos(): si 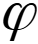 = 0 (barre verticale), une accélération de cet angle va accélérer le chariot (car la barre va vouloir tourner autour de son centre de gravité) (bon là ça devient plus tordu, je l’admets)
= 0 (barre verticale), une accélération de cet angle va accélérer le chariot (car la barre va vouloir tourner autour de son centre de gravité) (bon là ça devient plus tordu, je l’admets)
– ![]() : terme avec le sin(): le sin() est maximum quand
: terme avec le sin(): le sin() est maximum quand 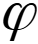 = 90°. A ce moment là, d’après l’équation, la vitesse de rotation (et même son carré) va tendre à diminuer
= 90°. A ce moment là, d’après l’équation, la vitesse de rotation (et même son carré) va tendre à diminuer ![]() . On peut l’expliquer (sûrement improprement diront les physiciens) par la force centrifuge de la barre, qui va tirer le chariot vers l’arrière)
. On peut l’expliquer (sûrement improprement diront les physiciens) par la force centrifuge de la barre, qui va tirer le chariot vers l’arrière)
Linéarisation des équations
Bon, le LQR est fait pour travailler avec des équations linéaires. Et là ce n’est pas vraiment le cas avec ces sin(), cos(), et carrés.
On utilise alors une astuce : on considère que dans notre problème, l’angle 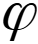 est proche de 0. Du coup
est proche de 0. Du coup
– sin( 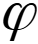 (t) ) =
(t) ) = 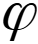 (t)
(t)
– cos( 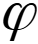 (t) ) = 1
(t) ) = 1
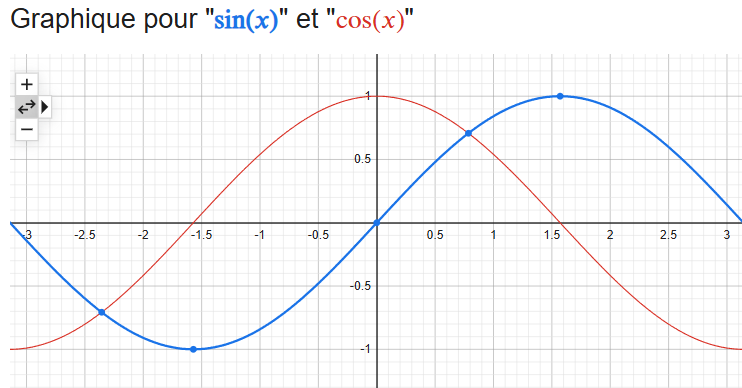
Autour de 0 :
– la fonction y=sin(x) est quasiment équivalente à la fonction y=x
– la fonction y=cos(x) est quasiment équivalente à la fonction y=1
et hop, ça simplifie bien les équations, qui vont alors devenir linéaires : les relations entre x, x’ et x », 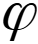 ,
, 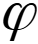 ‘,
‘, 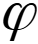 » seront linéaires (uniquement des multiplications et additions) :
» seront linéaires (uniquement des multiplications et additions) :
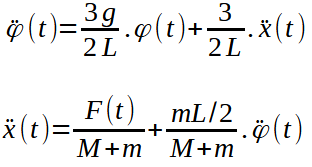
Le but est ensuite de séparer les accélérations des variables vitesse et position. Avec un peu de gymnastique mathématique simple, on arrive à :
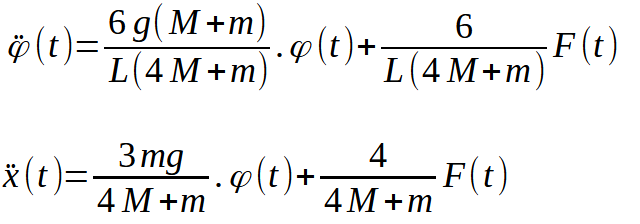
On peut écrire ces équations de la manière suivante :
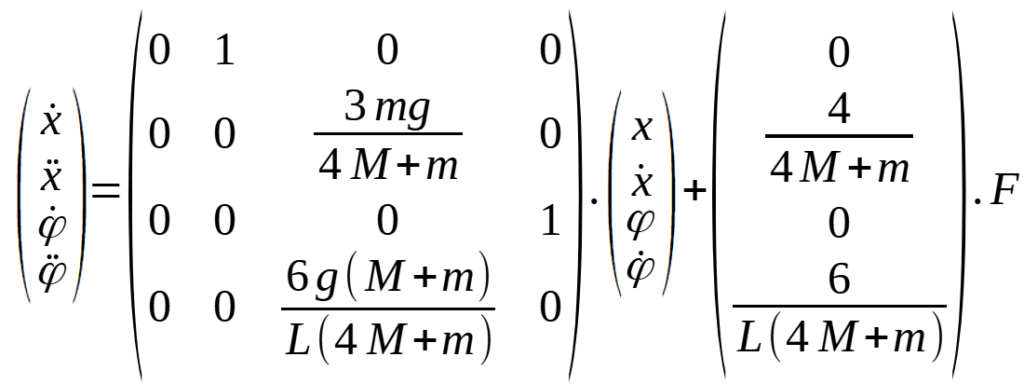
On peut donc finalement écrire :
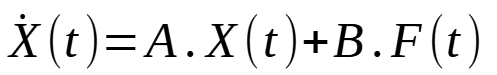
avec
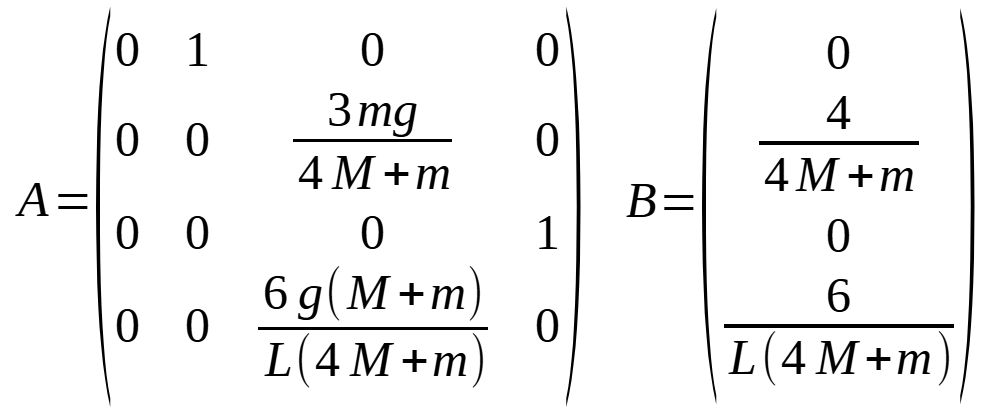
et donc
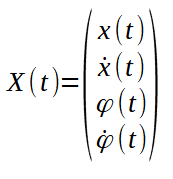
2 – Choix des matrices de pondération Q et R
Nous allons ensuite définir 2 matrices, qui permettent de « régler » la régulation.
La matrice Q donne un poids aux écarts :
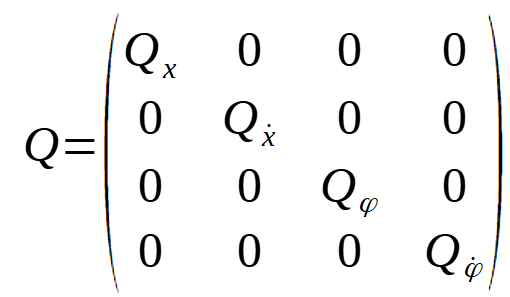
Pour chaque variable, une valeur est élevée signifie qu’il est prioritaire de corriger l’écart.
Exemple : ![]() est le poids de l’écart entre
est le poids de l’écart entre 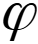 et 0 (çàd l’angle de la barre par rapport à la verticale)
et 0 (çàd l’angle de la barre par rapport à la verticale)
Idem pour les autres variables (et donc leurs vitesses)
Exemple ci-dessous : on donne un « poids » de 5 à la variable x, 1 à x’, 10 à 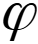 , 1 à
, 1 à 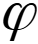 ‘.
‘.
Il est donc 5 fois plus important de ramener x à 0 que de ramener x’ (la vitesse du chariot) à 0.
Et il est 10 fois plus important de ramener 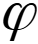 à 0 que de ramener x’ (la vitesse du chariot) à 0.
à 0 que de ramener x’ (la vitesse du chariot) à 0.
Etc…
Ces poids sont tous relatifs.
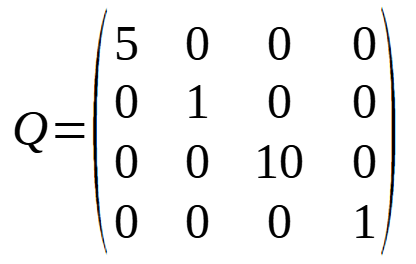
La matrice R « pondère l’effort de commande ».
Dans notre cas, la matrice R est un simple réel, car la commande est un simple réel aussi (ce n’est pas un vecteur)
Exemple: R = 0,01
Avec nos 4 matrices A, B, Q et R, on va pouvoir alors enfin (!) trouver comment commander notre système.
Il faut pour cela déterminer la « matrice de gain » K.
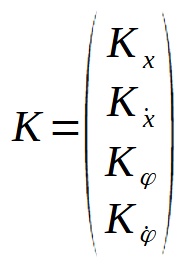
Pour cela il faut tout d’abord déterminer la matrice P solution de l’équation de Riccati suivante (ne vous inquiétez pas !!)
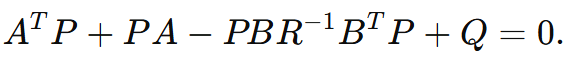
Une fois qu’on a P, on trouve K :
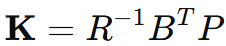
Mais tout ça ne se fait qu’une fois.
Si vous programmez en Pyhon, pour trouver K il suffit d’écrire :
P = solve_continuous_are(A, B, Q, R)
K = np.linalg.inv(R).dot(B.T.dot(P))
Si vous ne programmez pas en Python, pour trouver K il suffit de lancez les 2 commandes ci-dessus dans Google Colab (cela est documenté dans mon code) et vous obtenez le résultat, la matrice K, que vous aurez juste à saisir dans votre programme.
Car cette matrice K va enfin pouvoir nous servir concrètement dans le programme : elle nous sert à calculer la force permettant de maintenir les variables du vecteur d’état proche de 0 (selon les pondérations de la matrice Q) :
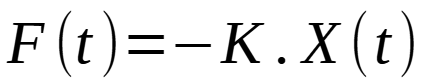
Dans mon cas avec
m = 0.3 # Masse du chariot (kg)
M = 0.3 # Masse du pendule (kg)
L = 0.67 # Longueur du pendule (m)
g = 9.81 # Gravité (m/s^2)
je trouve :
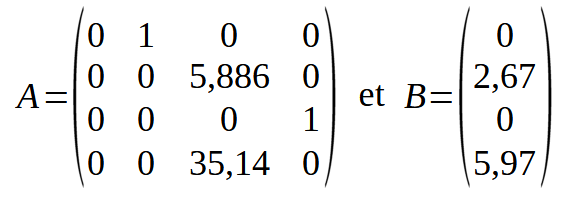
Et avec les matrices Q et R définis ci-dessus, Google Colab me trouve
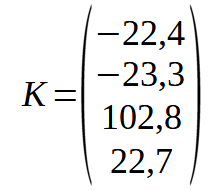
Cela donne finalement le pseudo-presque-code suivant, normalement très compréhensible :
void loop() {
// Mesures des positions
angleMesure=lectureAngle();
xChariotMesure=lectureXChariot();
// Mesure du temps dt
currTime=millis();
dt = currTime - prevTime; // Durée mesurée réelle de la boucle en ms (environ 50ms)
prevTime=currTime;
// Calcul des vitesses
vChariotMesure=(xChariotMesure-xChariotMesurePrecedent)/(dt/1000);
vAngleMesure=(angleMesure-angleMesurePrecedent)/(dt/1000);
xChariotMesurePrecedent=xChariotMesure;
angleMesurePrecedent=angleMesure;
u = - (-22.4 * xChariotMesure + -23.3 * vChariotMesure + 102.8 * angleMesure + 22.7 * vAngleMesure);
pMoteur = round(u*kU); // kU sert à adapter le résultat à la commande du moteur qui est comprise en -128 et +127
vitesseMoteur(pMoteur); // entre -128 et +127
}Quelques remarques
1 – On voit qu’on est quand même très proche d’un PID (pour ceux qui connaissent) ! Car on retrouve le Kp (-22,4 ici) et le Kd (-23.3 ici) Il manque juste la composante intégrale (mais il existe des LQR « adaptés » avec une composante intégrale)
2 – J’ai tenté ici une approche très « pragmatique » du LQR, sans la théorie. J’espère ne pas avoir écrit trop de bêtises car je ne maitrise pas trop cette partie théorique. Les calculs, eux, devraient être bons. N’hésitez pas à ajouter des commentaires si je n’ai pas été rigoureux dans mes explications, où s’il y a des erreurs.
3 – Concernant K, je suis parti des valeurs calculées, puis à l’aide du programme en C# j’ai modifié ces valeurs manuellement (à l’aide des curseurs sur l’IHM) pour finalement trouver les valeurs « idéales » pour mon système (et pour moi).

4 – Concernant les lettres « LQR »
- L=linéaire, car on part d’une équation de dynamique linéaire : X'(t)=A.X(t)+B.F(t). De plus la commande est aussi linéaire : u=-K.X
- Q=quadratique, car la « fonction de coût », celle que le LQR va tenter de minimiser, est fonction de x² et
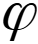 ² (cf. wikipédia, c’est la fonction J) (quadratique=fonction de puissance 2)
² (cf. wikipédia, c’est la fonction J) (quadratique=fonction de puissance 2) - R=régulation
Téléchargement
Code
Vous trouverez ci-dessous mon code qui comprend les répertoires suivants :
- C# : application à compiler sous Visual Studio, pour le PC
- CapteurRotation : programme à envoyer sur l’Arduino Uno relié au capteur de rotation
- CapteurXChariot : programme à envoyer sur l’Arduino Uno relié au capteur de rotation du moteur
- Remarque : les 2 programmes ci-dessous sont 99% identiques. Ils utilisent tous les deux la librairie PololuWheelEncoders.h (qui fonctionne très bien). La seule différence est que l’un des 2 définit ses pins d’entrée en INPUT_PULLUP, et l’autre en INPUT.
- Uno_Principale : programme pour l’Arduino Uno
Fichier 3D
Si vraiment vous voulez reproduire cette machine, voilà le fichier 3D :
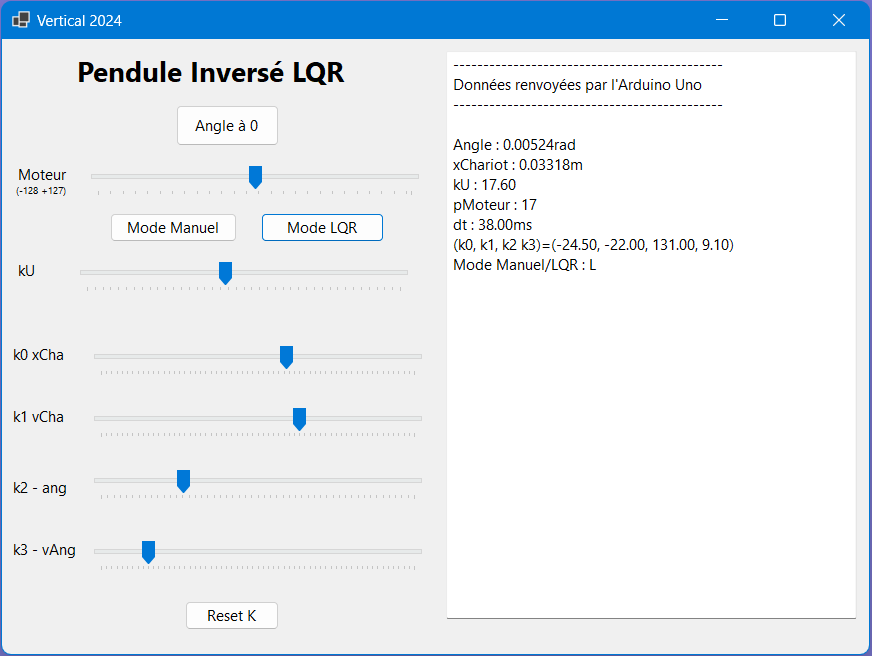
Lancement
Pour « initialiser » correctement le programme il faut définir les « 0 » des capteurs angulaires. Pour cela :
- tout brancher
- placer le chariot en milieu de sa course, faire un reset sur l’arduino du capteur du chariot -> son compteur se remet à 0
- placer la barre verticalement (c’est le plus délicat : il y a un très très léger frottement dans l’encodeur rotatif qui me permet trouver une position verticale quasi stable avec un peu de patience), faire un reset de l’arduino correspondant -> son compteur se remet à 0
- maintenir la barre presque verticale et appuyer sur le bouton « Mode LQR » de l’IHM sur le PC
Et là, la magie opère !







Bonjour, serait-il possible d’échanger avec vous par mails à propos de ce sujet dans le cadre d’un projet de TIPE en classes préparatoires?
bonjour
je suis en prépa PT et nous faisons un projet sur le pendule inversé dans lequel nous devons construire un prototype de pendule inversé sur chariot et nous avions quelques questions par rapport celui ci pourrions nous rentrer en contact
cordialement